十字相乘法是因式分解几种方法中的一种特殊方法,在一定条件下,用十字相乘法来解题的速度比较快,节约时间而且避免了大量运算,不容易出错。
一、十字相乘法概念
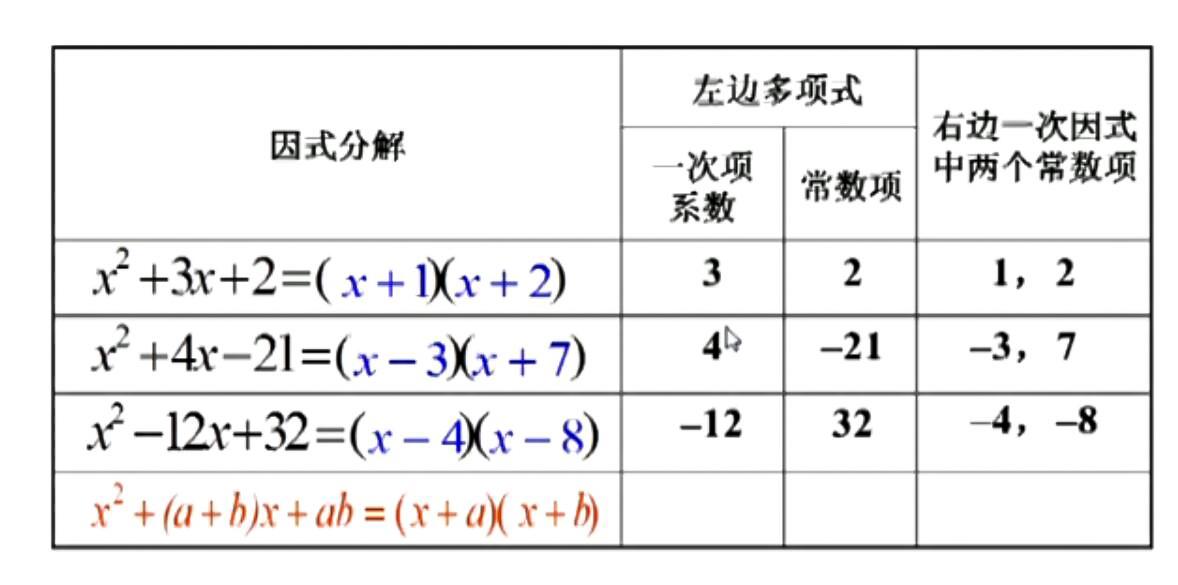
十字分解法的方法简单来讲就是:十字左边相乘等于二次项系数,右边相乘等于常数项,交叉相乘再相加等于一次项系数。其实就是运用乘法公式(x+a)(x+b)=x2+(a+b)x+ab的逆运算来进行因式分解。

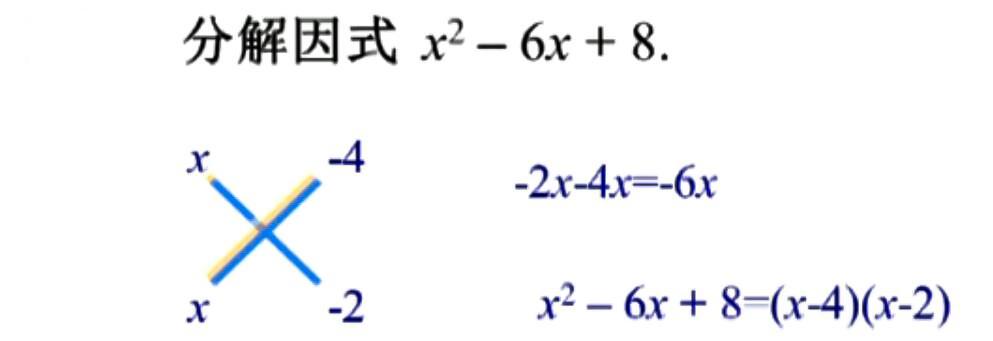
二、十字相乘法因式分解的一般步骤
(1)把二次项系数和常数项分别分解因数;
(2)尝试十字交叉图,使经过十字交叉线相乘后所得的数的和为一次项系数;
(3)确定合适的十字交叉图并写出因式分解的结果;
(4)检验。


二次项系数为1的多项式十字相乘法因式分解
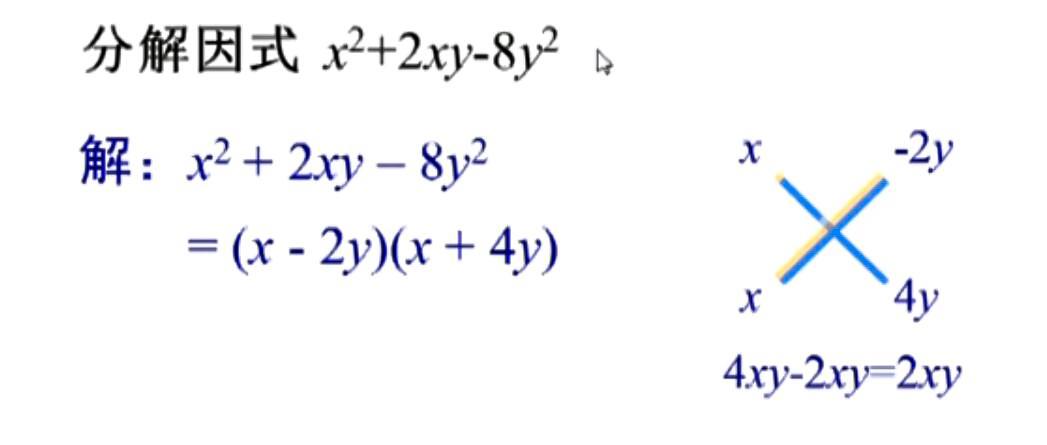
二次项系数为1的多项式十字相乘法因式分解
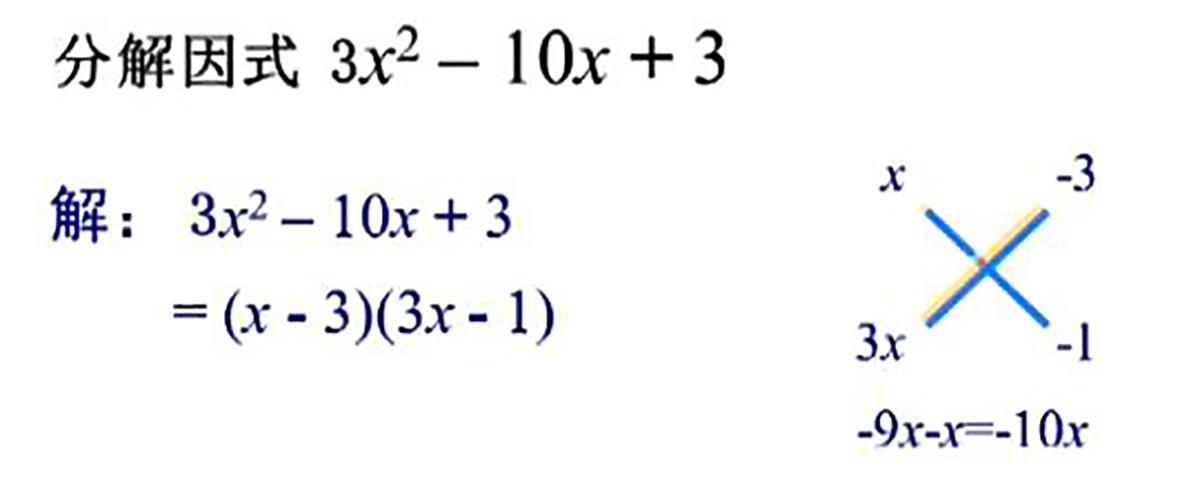
二次项系数不为1的多项式十字相乘法因式分解
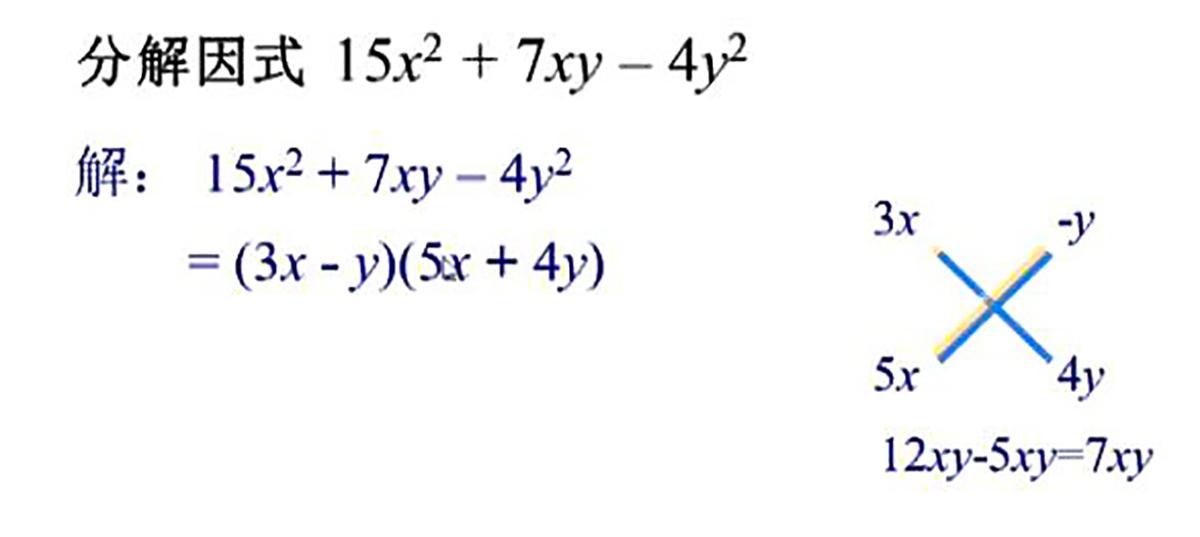
二次项系数不为1的多项式十字相乘法因式分解
三、十字相乘法的口诀
首尾分解,交叉相乘,求和凑中,平行书写。竖分常数交叉验,横写因式不能乱。
(1)竖分常数交叉验:
竖分二次项和常数项,即把二次项和常数项的系数竖向写出来;
交叉相乘,和相加,即斜向相乘然后相加,得出一次项系数;
检验确定,检验一次项系数是否正确。
(2)横写因式不能乱
即把因式横向写,而不是交叉写,这里不能搞乱。
