在WebGL的实际应用中我们广泛使用向量的几何运算来计算角度、距离,判断点线、点面之间的关系,比如物体之间的碰撞检测。
本文简要介绍三维计算机图形学中常用的基本运算的概念及其用途。
点积(Dot Product)
点乘比较简单,是相应元素的乘积的和:
V1( x1, y1, z1)·V2(x2, y2, z2) = x1*x2 + y1*y2 + z1*z2;
注意结果不是一个向量,而是一个标量(Scalar),可以是负数:
A·B = |A||B|Cos(θ)
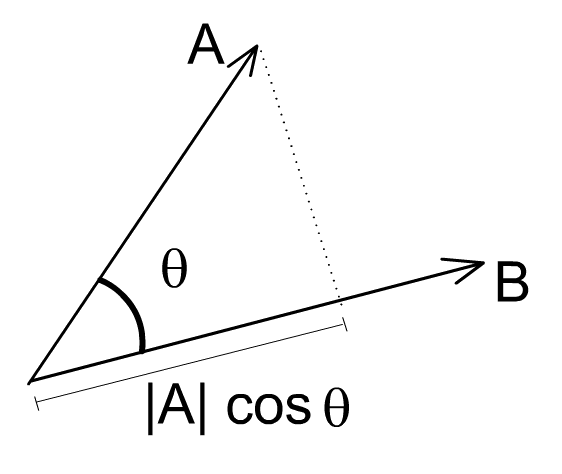
θ是向量A和向量B之间的夹角。这里|A|我们称为向量A的模或范数。这样我们就和容易计算两条线的夹角:
Cos(θ) = A·B /(|A|*|B|)
点积常见的用处是:
求线段在某个方向的投影长度(使B为单位向量)
计算两条线的夹角
计算点到线的距离(比如Math.sqrt(|A|*|A| - (A·B)*(A·B)),其中B为单位向量)
叉积(Cross Product)
首先我们知道 ,对于向量u和v, u x v的结果,是得到一个既垂直于u又垂直于v的向量,假设记作n.则有下面公式
n = u x v;
而n的方向,是由右手法则决定的。 即伸出右手,四个手指方向从u绕到v. 此时,大姆指的方向,就是n的方向。 我们通常叫做右向量。叉积常见用途有计算点到线和点到面的距离。
点到线的距离
找出一个点和一条线间的距离是经常遇见的几何问题之一。假设给出三个点,A,B和P,你想找出点P到点A、B定出的直线间距离。第一步是找出A到B的向量AB和A到P的向量AP,现在我们用该两向量的叉积除以|AB|,这就是我们要找的的距离了。
d = (AB x AP)/|AB|
(AB X AP)/2是三角形ABC的面积,这个三角形的底是|AB|,高就是P到AB的距离。有时叉积得到的是一个负值,这种情况下距离就是上述结果的绝对值。
当我们要找点到线段的距离时,情况变得稍稍复杂一些。这时线段与点的最短距离可能是点到线段的某一端点,而不是点到直线的垂线。
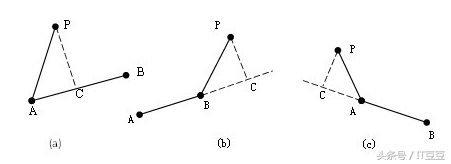
例如上图(b)中点P到线段AB的最短距离应该是线段BP。我们有几种不同的方法来判断这种特殊情况。
第一种情况是计算点积AB·BP来判定两线段间夹角。如果点积大于等于零,那么表示AB到BP是在-90到90度间,也就是说P到AB的垂线在AB外,那么AB上到P距离最近的点就是B。同样,如果BA·AP大于等于零,那么点A就是距离P最近的点。如果两者均小于零,那么距离最近的点就在线段AB中的某一点。
点到面的距离
设某三维平面表达式为
a*x+b*y+c*z+d = 0;
则其法向量即为: (a,b,c).
任意一点 p = (x1, y1, z1)到该平面的距离为:
(a*x1 + b*y1 + c*z1+d) / (a*a + b*b +c*c)
